
Finding us in homolog.us
Yes, you guessed it right. We shall discuss Burrows-Wheeler transform, which is behind many efficient RNAseq mapping algorithms like BWA, Bowtie and SOAP2.
What is a transform?
A transform is a set of rules to turn one thing into another. A recipe for making bread is a good example. You start with flour, yeast, water and salt, follow the rules, and have fresh bread out of the oven. Those, who are not particularly hungry, can try ‘count of nucleotides’ transform. This transform takes a long sequence and reports the number of As, Cs, Gs and Ts.
Reversible transform
A reversible transform turns A to B following a set of rules, but another set of rules can be derived to turn B into A. Have you seen anyone get flour and yeast out of bread? No. You are correct; making bread is not reversible. Neither can anyone reconstruct the original sequence in the above example from its count of nucleotides - 3As, 3Cs, 4Gs and 5Ts. The transform for converting nucleotide space data to SOLiD color space is another good example of irreversible transform.
Here are couple of reversible transforms -
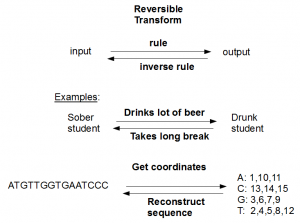
The first example above does not need any explanation, and so we proceed to the second. Suppose you have a transform that takes a long sequence and notes the locations of various nucleotides. It is always possible to reconstruct the original sequence from the location data. The transformation is reversible.
Burrows-Wheeler Transform
Burrows Wheeler Transform (BWT) is a reversible transform. It starts with a sequence or other type of text, and turns it into something else. BWT is useful, because the transformed sequence can be compressed far more easily than the original sequence. The popular bzip2 algorithm for file compression uses this transform. By the same token, transformed sequence can be loaded with much less RAM than the original sequence. This is important for mapping of RNAseq reads, because one can load the transformed human genome into the RAM of a laptop and do search for millions of Illumina reads.
How is the transform done?
Let us consider the word ‘homolog.us$’. We added the character ‘$’ at the end, because inverse BWT is reversible only up to giving the circular sequence and does not give the begin and end of original sequence. With ‘$’ marking the end of the sequence, it becomes trivial to identify the begin and end from the circular sequence.
To transform ‘homolog.us$’, the same word is written 11 times with one letter sent from front to back in each iteration.

Please note that each row and each column has all characters of the word ‘homolog.us$’ by way of construction.
In the following step, all 11 lines (rows) in the above matrix are sorted alphabetically. The last line (‘$homolog.us’) starts with ‘$’ and moves to the top. Then comes (‘.us$homolog’) and so on. The sorted matrix is shown below, and you can see that the characters in the first column follow alphabetic order as it should be with any sort. The lines with identical characters in the first place (‘og.us$homol’, ‘olog.us$hom’ and ‘omolog.us$h’) got sorted on the basis of second characters. Do make a mental note of the above point, because it is important in understanding LF mapping property explained below.
After sorting is done, last column (‘sg$oolmhu.’) is called the BWT transform of the original sequence (‘homolog.us$’). Note again that each column always has all characters of ‘homolog.us$’, because sorting does not change the columns but only rearranges them. Also note that the first column is a sorted list of all characters in ‘homolog.us$’.

Why is BWT useful?
If you transform a very long sequence, BWT brings similar characters together and makes it more efficient to compress them. For example, you see that in the transformed sequence, two ‘o’s are brought together and the third ‘o’ is nearby.
Second property of BWT is useful for performing nucleotide searches. It is called last-to-front mapping (LF mapping). To explain it, we perform the same transform as above, but mark three ‘o’s in different colors.
Here is the original list -

Here is the sorted list -

LF mapping property says that the order of nucleotides in the first column is the same as order of nucleotides in the last column even up to the colors of nucleotides. You can see that three ‘o’s in the first column are sorted as blue, green and red. In the last column, which is the BWT transform of the original sequence, blue ‘o’ came first, green ‘o’ came second and red ‘o’ came third. Please check these slides, if you want to understand LF mapping property mathematically.
There is nothing magical about LF mapping property and you can understand it by just thinking through the sorting process. Three ‘o’s of the last column are followed by characters ‘g’, ‘l’ and ‘m’ in the first column. They are sorted with ‘g’ followed by ‘l’ followed by ‘m’, because first column sorts the characters.
Three ‘o’s of the first column are followed by the same ‘g’, ‘l’ and ‘m’ in the second column. When those lines are sorted, the first column is the same (‘o’), and therefore the sorting order is decided by the second column.
The implications of LF mapping property are profound, as we shall see in the next commentary describing Bowtie search algorithm.