
Finding us in homolog.us - part II
We explained the basics of Burrows-Wheeler transform in our previous commentary. Here we present another example - ‘tatatatata$’. Just like before, you need to write the word many times with one letter shifted to the back until all letters have been shifted.

Following table is obtained by sorting the above table alphabetically. The last column gives the Burrows Wheeler transform of the original sequence. Again you see that all Ts and all but one As are clustered together in the transformed sequences.

In the above tables, all As and Ts of the original sequence have different colors so that one can track where they ended in the final sequence. You can see that the color-ordering of As in the last column is the same as the color ordering of As in the first column. Ts also show similar property known as LF mapping property.
We mentioned that BWT is reversible. How do we go back from the following sequence to ‘homolog.us$’ ?

Please note that the above sequence comes from the last column of matrix to derive BWT, but we also know another column, the first one. The first column has all characters of the last column sorted alphabetically.
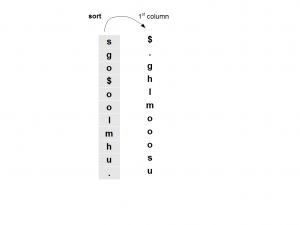
What else do we know? We know that, in the original word, the characters in the first column follow the characters in the last column. So, we know that in the original word ‘s’ is followed by ‘$’, ‘g’ is followed by ‘.’, ‘o’ is followed by ‘g’, ‘$’ is followed by ‘h’, ‘o’ is followed by ‘l’ and so on.
The letter followed by $ is the first word. That is ‘h’. Then comes ‘o’ from the above table. What comes after ‘o’? We have three choices - ‘g’, ‘l’ and ‘m’. This is where we need to invoke the LF mapping property. We know that ‘h’ is followed by the last ‘o’ in the 1st column. The last ‘o’ of th BWT column is followed by ‘m’. Pretty neat, huh? You can reconstruct the entire sequence in this manner.
One last thing - we forgot to answer the original question of whether ‘us’ exists in ‘homolog.us’. We start with the character ‘u’ in the above table, and find that it is present only once and is followed by ‘s’. We found ‘us’ in ‘homolog.us’ !!!