
Hardware-based Hash Functions
The purpose of hashing is to map sparse data spreading over large potential address space into a smaller address space.
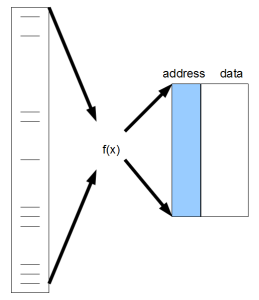
Choosing the right hash function requires some creativity, and at times so much so that companies choose to patent their creative hash functions. To patent a hash function, you need three things -
(i) a function that is reasonably random, when it assigns entities in large address space to small address space,
(ii) a function that runs fast,
(iii) an aggressive company backing you.
Some others cite patenting of hash functions as the US patenting office going amock.
We have been looking for few good hardware-based hash functions and came across this wonderful website maintained of Bob Jenkins as part of his larger website.
Bob mentioned a nand-based hash on his webpage.
Mark Spitzer was asking how to do a hash in hardware. The file nandhash.c simulates a hash I’ve designed for hardware.
It has 2x4 blocks of 4x4 bits apiece, for a total internal state of 128 bits. A single round first XORs a few bits to other blocks horizontally and vertically, then does a reversible nonlinear mixing of each 4x4 block. The 4x4 mix is actually a linear LFSR on bits 0..7 that XORs 3 or 4 bits per bit, while doing ~b^((w&x;)|(y&z;)) on bits 8..15, then swapping bit i with bit 15-i. I count a single round at being 9 NANDs deep. I skimped on long wires because I’ve heard they’re slow and take lots of room.
To measure it, I started from a random state, made a copy with one bit flipped (0,0,14, which measurements suggested was the worst case), running both for n rounds, then XORing the results. I updated a count for every bit that changed. I did that 100,000 times, divided by 100,000, to get a probability p for each bit. Ideal is p=0.50.
Other useful ideas -
Linear feedback shift register

In computing, a linear feedback shift register (LFSR) is a shift register whose input bit is a linear function of its previous state.
The most commonly used linear function of single bits is XOR. Thus, an LFSR is most often a shift register whose input bit is driven by the exclusive-or (XOR) of some bits of the overall shift register value.
The initial value of the LFSR is called the seed, and because the operation of the register is deterministic, the stream of values produced by the register is completely determined by its current (or previous) state. Likewise, because the register has a finite number of possible states, it must eventually enter a repeating cycle. However, an LFSR with a well-chosen feedback function can produce a sequence of bits which appears random and which has a very long cycle.
Applications of LFSRs include generating pseudo-random numbers, pseudo-noise sequences, fast digital counters, and whitening sequences. Both hardware and software implementations of LFSRs are common.
Specification of a CRC code requires definition of a so-called generator polynomial. This polynomial resembles the divisor in a polynomial long division, which takes the message as the dividend and in which the quotient is discarded and the remainder becomes the result, with the important distinction that the polynomial coefficients are calculated according to the carry-less arithmetic of a finite field. The length of the remainder is always less than the length of the generator polynomial, which therefore determines how long the result can be.
In practice, all commonly used CRCs employ the finite field GF(2). This is the field of two elements, usually called 0 and 1, comfortably matching computer architecture.
The simplest error-detection system, the parity bit, is in fact a trivial 1-bit CRC: it uses the generator polynomial x+1.
You may also find following links useful.
1. A stackoverflow discussion thread
2. An old paper - Hardware design for Hash functions - Y. K. Lee et al.
3. An even older paper - A Design Principle for Hash Functions
4. Efficient Hardware Hashing Functions for High Performance Computers
If you are still unable to proceed, please send us email at samanta at homolog.us and we will help you design one.