
Performing Burrows Wheeler Transform on Trees
Dear reader, if you are looking for a way to assemble the genome of a tree, you are at the wrong thread, and please check here instead. Trees of today’s discussion live inside computers and grow by consuming electrical energy, not energy from the sun.
We have been going through the well-written blog post of Alex Bowe - Succinct de Bruijn Graphs. The topic has been covered in our blog here and here.
One important idea of their work came from a different paper and we think it is worth mentioning in a separate commentary, because the concept is fascinating and is not restricted to de Bruijn graphs. Storing and traversing through graphs is a major problem in computer science, and the way of storing it as compact linear arrays can possibly help us get rid of pointers.
Compressing and Indexing Labeled Trees, with Applications
We present a new approach to indexing labeled trees without pointers that supports all the operations stated above in (near-)optimal time and achieves succinctness not only in information-theoretic sense, but also at a deeper level of the entropy of the input. This will lead us to compressed indexes for labeled trees. Our results are based upon a new XBW-transform of the labeled tree T , denoted by xbw[T ], which linearizes the tree into two coordinated arrays hSlast, S?i, one capturing the structure and the other the labels of T . These two arrays are compressible and ef?ciently searchable, and thus let us transform compression and indexing problems on trees into well-understood problems on strings. xbw[T ] has the optimal size of 2t + tlog|?| bits (Theorem 1) and can be built and inverted in optimal linear time (Theorems 2 and 3). In designing the XBW-transform we were inspired by the elegant Burrows Wheeler transform (BWT) for strings [Burrows and Wheeler 1994]. In the past few years, the BWT has been the unifying tool for string compression and indexing, producing many important breakthroughs [Ferragina et al. 2005; Navarro and Makinen 2007]. In the spirit of BWT, which relies on suf?x sorting for grouping together similar symbols of the input string, our XBW-transform relies on path sorting to linearize and group the labels of T within the two coordinated xbw[T ]s arrays.
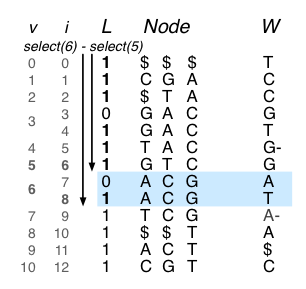
If you find the paper difficult to follow, Alex has worked out a complete example that is fairly easy to understand, provided you know how BWT and FM indices work. Only thing to note from today’s commentary is that this beautiful idea can be applied to all forms of graphs, not only those related to genome assembly.