
Plactic Monoid, Schubert Polynomial and Combinatorics of Words
A few months back, we came across a set of informative slides from Amy Glen, an Australian mathematician, but did not have time to dig into the details. You can click on the image to see the slides.

Finally we are starting to go through all relevant topics to fully understand the slides. If this commentary appears like a bunch of random definitions and links, that is what it is. We are simply making a note of all relevant links here to go through the topics covered in them over the next 6-7 months.
-———————————————-
1. Marcel-Paul Schtzenberger
Schtzenberger was an eminent French scholar, who first did his PhD in medicine and then in mathematics. Over his long career, he made very deep contributions in combinatorics and information theory. We will come across a number of his papers in the following links. Until the end of his life, he doubted the evolutionary theory of Mayr and others, also known as ‘modern synthesis’. In our very personal opinions, horizontal gene transfer (reticulate evolution) takes care of the objections he had. However, the evolution of eukaryotic cells from prokaryotic cells is still a mystery. Dan Graur wrote a detailed commentary on that topic.
-———————————————-
2. Combinatorics Books by M. Lothaire
M. Lothaire is an eminent French mathematician, who does not exist. The students of
Schtzenberger joined together to write books under the above pseudonym (copying the tradition of N. Bourbaki). They have three books so far.
Algebraic Combinatorics on Words
Applied Combinatorics on Words
-———————————————-
3. Plactic Monoid
What is a monoid? They are groups minus inverse property.
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are semigroups with identity. Monoids occur in several branches of mathematics; for instance, they can be regarded as categories with a single object.
The following image from wiki page on groups describes all group and group-like structures.
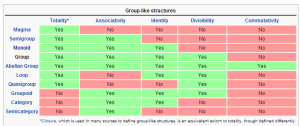
Those interested in group theory should check out the following project, which appears like the ‘human genome project of group theory’.
Classification of finite simple groups
Finally, here is the definition of plactic monoid -
In mathematics, the plactic monoid is the monoid of all words in the alphabet of positive integers modulo Knuth equivalence. Its elements can be identified with semistandard Young tableaux. It was discovered by Donald Knuth (1970) (who called it the tableau algebra), using an operation given by Craige Schensted (1961) in his study of the longest increasing subsequence of a permutation.
It was named the “monode plaxique” by Lascoux & Schtzenberger (1981), who allowed any totally ordered alphabet in the definition. The etymology of the word “plaxique” is unclear; it may refer to plate tectonics (tectonique des plaques in French), as the action of a generator of the plactic monoid resembles plates sliding past each other in an earthquake.
Monoid factorisation and Schtzenberger theorem
-———————————————-
4. Representation theory
Representation theory converts all group theory problems into linear algebra problems. Since the later subject is well studied, the conversion helps in solving problems from the former subject.
Conceptually it is like coordinate geometry+trigonometry, which is used to solve geometry problem by translating them into algebraic problems. Some mathematicians do not like solving problems in one domain by using machinery in other domain, because often the elegance of mathematics is lost. Ivan Niven’s “Maxima and Minima without Calculus” is a fascinating book on that topic.
Maxima and Minima Without Calculus (Dolciani Mathematical Expositions)
On the other hand, Wiles solved Fermat’s last theorem (a number theory problem) by using techniques in algebraic geometry. What is good for the gander may not be good for the goose here :)
-———————————————-
5. Schubert and Schur polynomial
Schur polynomials are certain kinds of symmetric polynomials with very special properties.
Schubert polynomials are generalization of Schur polynomials.
Relevant paper is available here.
Also check -
Combinatorial aspects of the LascouxSchutzenberger tree by David P. Little
-———————————————-
Where do they all fit?
Thanks for asking. A string of concatenated characters or words is a good example of monoids. They follow associative rule, but not any other property of groups. Therefore, it is interesting to check their general mathematical properties in terms of factorization.
After all, factorization of large strings is useful in parallelizing the construction of large BWT structure, such as a large genome or large Illumina library).