Only three driver gene mutations are required for the development of lung and colorectal cancers

Tomasetti, Vogelstein and co-authors recently published another informative paper on somatic mutations and cancer, but it got lost due to cacophony related to their Science paper. This paper has a lot more details on their mathematical model.

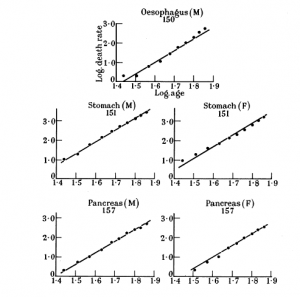
Cancer arises through the sequential accumulation of mutations in oncogenes and tumor suppressor genes. However, how many such mutations are required for a normal human cell to progress to an advanced cancer? The best estimates for this number have been provided by mathematical models based on the relation between age and incidence. For example, the classic studies of Nordling [Nordling CO (1953) Br J Cancer 7(1):6872] and Armitage and Doll [Armitage P, Doll R (1954) Br J Cancer 8(1):112] suggest that six or seven sequential mutations are required. Here, we describe a different approach to derive this estimate that combines conventional epidemiologic studies with genome-wide sequencing data: incidence data for different groups of patients with the same cancer type were compared with respect to their somatic mutation rates. In two well-documented cancer types (lung and colon adenocarcinomas), we find that only three sequential mutations are required to develop cancer. This conclusion deepens our understanding of the process of carcinogenesis and has important implications for the design of future cancer genome-sequencing efforts.

Speaking of criticism about the Science paper, the biggest part of nonsense comes from Yaniv Erlich, a poorly trained technician at Broad Institute, who keeps harping on their use of log-log distribution. Folks, log-log distribution has been used in cancer literature related to somatic mutations since the 1950s, such as these two classic papers - A New Theory on the Cancer-inducing Mechanism - C. O. Nordling and The Age Distribution of Cancer and a Multi-stage Theory of Carcinogenesis - P. Armitage and R. Doll. Everyone knows that it represents y=x^a type of mathematical relationship, including Nordling, who mentioned in his paper and Tomasetti et al., who reproduced the math of Armitage and Doll in their PNAS paper.

We believe Yaniv Erlich should stick to showing his ignorance on read coherence rather than diversifying into many different areas.