
An Intuitive Explanation for Running Velvet with Varying K-mer Sizes
We often run Velvet or other de Bruijn assemblers with varying K-mer sizes (21, 23, 25, 27, etc.) to find the best assembly. Why does the method work? Let us present an intuitive explanation.
One of our earliest commentary on de Bruijn graphs contained the following graph -
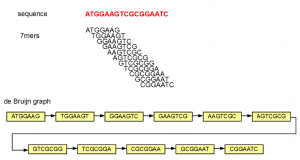
If someone gives you the de Bruijn graph at the bottom of the figure, would you be able to reproduce the underlying sequence (red)? The answer is yes, because each 7-mer has unique neighbors, from which the next nucleotide can be determined. If all de Bruijn graphs were like the above figure, genome assembly would have been an easy problem. In reality, we encounter de Bruijn graphs with many criss-crosses, originating primarily from the repetitive regions of a genome.
Here is a simple example of two overlapping branches of a de Bruijn graph.
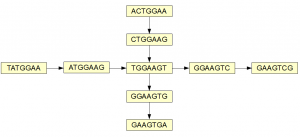
The graph can be traversed through four paths (shown below in four colors), but are they all real? When we inspect the underlying sequence, we find that only the red and green branches have supporting evidence.
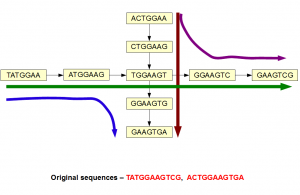
The above picture is a good example of a scenario, where information is lost after constructing de Brujin graph. The original sequences were likely from non-repetitive regions of a genome, but they happened to have a common k-mer. That common k-mer made two branches overlap, giving the assembler four paths to resolve instead of two.
You can see that two paths would separate by simply going from 7-mer to 9-mer. Increasing k-mer size resolves many spurious ambiguities thus making the task of assembler easier.