
HapCompass: An Elegant Use of Graphs for Haplotype Assembly/Phasing
We came across an interesting paper on haplotype assembly from NGS data titled HapCompass: a fast cycle basis algorithm for accurate haplotype assembly of sequence data. It is from Sorin Istrail’s group at Brown University.
A diploid organism has two copies of nearly identical chromosomes, but almost all de Bruijn graph-based assemblers discussed previously (De Bruijn graphs I, De Bruijn graphs II, De Bruijn Graphs III, remaining de Bruijn graph series) start with the assumption that those chromosome pairs are identical. That is a very good starting point, when no genome exists and the primary task is to assemble the genome de novo. Far more work is needed to assemble rare group of highly polymorphic genomes, and algorithms like HaploMerger presented earlier or colored de Bruijn graphs can help.
HapCompass applies for a different class of problems. Plans are underway to sequence the chromosomes of thousands of human individuals, and next-gen sequencing is dramatically reducing the cost of that effort. Constructing reference genome is not an issue for humans, because major sequence projects already built ‘reference’ genomes of people from various parts of the world. The key question is how the genomes of various individuals differ from that reference, and even more importantly whether it is possible to deconvolute reads data to assign SNP differences to two different chromosomes. The point is illustrated in the following figure, where we show locations of two SNPs for an individual. Finding the locations of SNPs is easy, because it requires mapping all reads to the reference, and finding locations that differ from the reference.
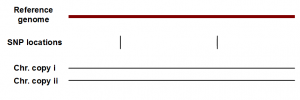
In the above figure, two SNPs can both be on chromosome copy i, both on copy ii, or one on i and one on ii. Assigning all SNPs to two different chromosomes is difficult, and the problem is even harder for NGS sequences.
There are three ways to answer the above question.
(i) GATK type of mapping-based method - Use mapping-based methods to map all reads, and then use GATK tools to decolvolute SNPs. GATK finds whether two SNPs from distant locations are on the same pair of mate pairs, and assigns them to the same chromosome accordingly.
(ii) De Bruijn graph-based de novo assembly - De novo assembly methods are extended to include haplotype difference by adding ‘color’ to the graph. We will discuss the Iqbal et al. paper in a different commentary, but as a quick note, de Bruijn graph-based methods can become cumbersome near SNP sites, because each SNP turns into a ‘bubble’ with two alternate paths. It is not straightforward to use long-range connectivity of mate-pairs to connect two bubbles.
(iii) HapCompass - The novelty of HapCompass is to create a different kind of graph (named ‘compass’ in the paper) that assigns SNPs as nodes and linking paired-end sequences as edges. In the following figure, if two SNPs come from the same chromosome, they will be linked by an edge. If not, no edge will exist between them. Of course, the previous statement assumes complete error- free world. Few spurious edges can be created by noisy sequence data.
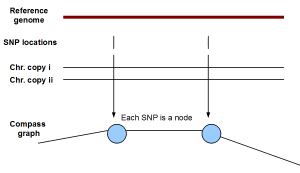
Based on the above graph structure, the authors translated the phasing/haplotype assembly problem into a spanning tree problem, and solved it through a minimum weight edge removal optimization algorithm. It is a ‘happy’ merger of computer science and biology.

Few older related papers we would like to read, when we have time -
Optimal algorithms for haplotype assembly from whole-genome sequence data
Haplotype assembly from aligned weighted SNP fragments
An MCMC algorithm for haplotype assembly from whole-genome sequence data