
What are the Puzzle Pieces in a Rectangle Graph?
If playing chess against one Russian grandmaster is difficult enough, imagine doing the same against sixteen. That was the kind of trouble we got ourselves into over the weekend, when we tried to figure out the SPAdes code. Here is the good news - the game is still on and we have not accepted defeat yet :)
We wrote few times earlier about the SPAdes assembler, but never explained the rectangle graph algorithm.
From de Bruijn Graphs to Rectangle Graphs for Genome Assembly
Starting to Understand the SPAdes Papers
Heads Up for Readers SPAdes vs Ray Benchmarking is Done
In this commentary and next, we will cut to chase quickly and get to the core of the rectangle graph method.
Rectangle graph algorithm starts, where Minia and Meraculous left. If a de Bruijn graph looks like the following figure, Minia focuses on finding out the nucleotide regions between the branching nodes, or the regions A,B,C,D,E,F,G,H. The question is what next?
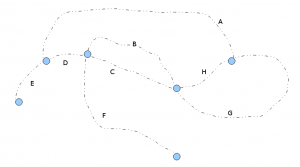
We explained the de Bruijn graph of repetitive regions earlier. In a repeat-rich genome, the above de Bruijn graph can code for many different genomes. For example, you can go around the loop of B, C multiple times before continuing with the remaining traversal. Rectangle graph algorithm presents an elegant method for deriving those repetitive structures in the genome based on mate- pair and paired end reads.
Explaining the algorithm will take more than one commentary, and today we only have time to explain what the puzzle pieces are.
In rectangle graph algorithm, the assembled pieces A to H are called h-edges, and the rectangular puzzle pieces consist of various combinations of A to H as two sides of rectangles. For example, A, A forms a rectangle (square), whose sides are of length(A) in nucleotide terms. A, B forms a rectangle with sides of length(A) and length(B). B, A can form a separate rectangle with sides of length(B) and length(A). In total, you have N*N possible rectangular pieces, and the genome assembly problem is equivalent to placing those pieces properly on a large square grid based on read pair information.
Please note that most of N*N combinations are not likely to be present in a genome assembly problem. Only those h-edges spanned by paired reads need to be considered. That greatly reduces the number of potential puzzle pieces we need to play with. It will be clear, when we explain the details in a follow-up commentary.