Genome Assembly from Random Sequence

In our tutorial section, we mentioned that genome assembly problem would not have become a real issue, if genomes were truly random sequences. Michael Schatz presents a detailed example in the attached twitter conversation.

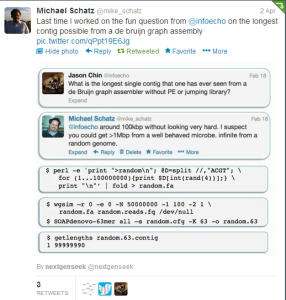
What is the mathematics behind above calculation? If we split a random genome into k-mers (k=63) and construct a de Bruijn graph, all k-mers are different due to randomness of the genome. We start getting duplicate k-mers, only when the genome size reaches the order of 4^63 (=8e37). If k-mers are not repeated in the genome, de Bruijn graph will be able to assemble the entire genome without any problem.

Real genomes are far from random and that is where the assembly challenge lies.

-—————————

Edit. That comment about getting duplicates only after genome size was close to 8e37 was sloppy, as Michael Schatz and Pall Melsted pointed out. We inserted ‘of the order of’ with some idea of that sort, but did not work out the numbers.

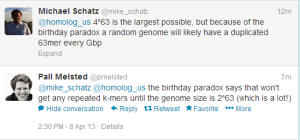
For those unfamiliar with birthday paradox, here is an old blog commentary.