
Burrows-Wheeler Transform (BWT) is de Bruijn Graph is BWT
The title is a bit of over-simplification to make a point. However, the strong connection between dBG and BWT becomes clear, when you understand the ‘succint de Bruijn graph’ method presented by Alex Bowe. We will encourage you to read the linked well- written commentary first. Following discussion presents the conceptual details that may help you understand what is going on.
Burrows Wheeler Transform
We covered Burrows Wheeler transform in the following two commentaries.
Finding us in homolog.us part II
Essentially you start with a word and keep rotating it by moving one character from front to back until all possibilities are exhausted. You end up with a table like this.

Sort all the entries in the table and take the last column. That is your Burrows Wheeler transform of the original word.

LF property is one important aspect of the transform. It is explained in detail in the above two linked commentaries.
De Bruijn Graph
Here is the de Bruijn graph (partial, genome assembly style) of the same word.
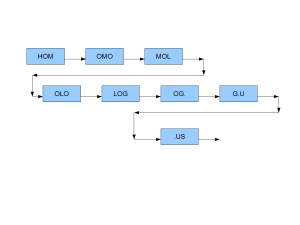
Do you see some similarity with the first table? The first node starts with the same characters as the first line in the table. Second node starts with the same characters as the second line, and so on.
So, if all nodes are different and you sort the nodes, the edges will form Burrows Wheeler transform and maintain LF property. That is how Alex Bowe’s method works.
However, there is a big difference. The three letter nodes are truncated versions of the full word, and that means, for many words, sorting would not work as perfectly as during formation of BWT. What will those imperfectly sorted nodes do to the de Bruijn graph structure? They will create branching k-mers. The additional arrays in Alex’s data structure are used to keep track of those branching k-mers. For example, if you take his 0/1 bit array and remove all ‘0’ edges, you will get a perfect linear chain like above.
Lyndon Word
We are not the first to notice the similarities between BWT and dBG. We discussed about Lyndon words and Lyndon factorization in connection with Burrows Wheeler transform, and the wiki page on Lyndon word explains its connection to dBG.
Connection to de Bruijn sequences
If one concatenates together, in lexicographic order, all the Lyndon words that have length dividing a given number n, the result is a de Bruijn sequence, a circular sequence of symbols such that each possible length-n sequence appears exactly once as one of its contiguous subsequences. For example, the concatenation of the binary Lyndon words whose length divides four is
0 0001 0011 01 0111 1
This construction, together with the efficient generation of Lyndon words, provides an efficient method for constructing a particular de Bruijn sequence in linear time and logarithmic space.[11]
So, Lyndon words may be useful in simplifying dBG. How that works will be the topic of a future commentary.
-——————————————————-
Edit. Those, who are wondering about how these esoteric topics help in sequence analysis, BWT can be useful in compressing the de Bruijn graph into smaller memory so that you are spared from buying 512GB server and Lyndon word may help in partitioning the BWT (=faster construction).