De Bruijn Graphs for Alternative Splicing and Repetitive Regions
Today we shall examine de Bruijn graphs for two structures that occur frequently in genomes or transcriptomes. The reason for studying them together will be apparent by the end of this post.
Let us first construct a graph for two alternatively spliced transcripts A and B for a gene. The regions shown in yellow and red are transcribed in both isoforms, whereas the green region is present only in A.
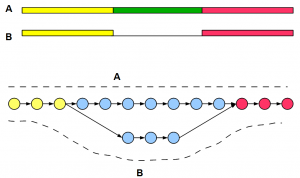
The de Bruijn graph is shown in circle and arrow format, and the paths for two transcripts are marked by dotted lines. We shall explain the graph construction qualitatively instead of going into nucleotide level detail. We recommend you to pick your favorite gene and do the detailed construction yourself by following rules explained earlier.
For large parts of yellow and red regions, K-mers are common between two transcripts. Therefore, their de Bruijn graph will connect sets of common nodes. The green region of A will generate many new K-mers and follow a path similar to blue upper branch of the de Bruijn graph. It is important to note that B will also generate K-mers not present in A. They are junction K-mers spanning between yellow and red junctions. Hence, de Bruijn graph of B will follow lower blue branch.
Next, we construct de Bruijn graph for repetitive segment of a genome. In the following figure, two green regions are identical and yellow, blue and red regions are all distinct.
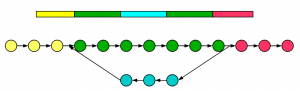
The de Bruijn graph for the segment is also shown with nodes for different regions marked in respective colors. The coloring is somewhat simplified, because it paints various junction K-mers with single colors. However, the topography of construction is accurate, and we recommend you to pick a simple example and try the construction yourself.
From a cursory look of above figures, you may think that de Bruijn graphs of alternatively spliced genes and repetitive segments are identical. Are they?
Please pay close attention to the direction of the arrows and you will see the difference. De Bruijn graphs are directed graphs, where flipping an arrow can completely change the meaning of the graph. For alternative splicing, all arrows are going from left to right. For repetitive structure, arrows connecting blue circles in the figure go from right to left.
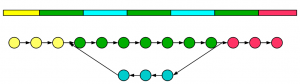
Another interesting observation the first graph can be uniquely resolved into structures A and B, but the second graph cannot. For example, the de Bruijn graph of the following repetitive genomic segment also has the same de Bruijn structure as one considered earlier. Therefore, the graph shown here can resolve to many possible structures in nucleotide space. This multiplicity appears from presence of loop in the de Bruijn graph.
How do sequencing errors affect de Bruijn graphs?
A Drawback of de Bruijn Graph Approach
Using Mate Pair Information in de Bruijn Graphs
Do de Bruijn Assemblers Work in Color Space?
