
An Opinionated History of Genome Assembly Algorithms - (i)
Dear readers,
Please stop telling us by email that Gene Myers was not pleased to read our summary of his Dazzler assembler talk. Our commentaries are not written to please anyone, and even less so, when we try to quickly ‘assemble’ a coherent narrative from over two hundred tweets.
For that matter, neither are our commentaries written to displease any serious scientist (a qualifier that excludes ENCODE ‘leaders’), and we like to present the truth as accurately as possible. Therefore, for the benefit of the community, we will dig into the history of genome assembly algorithms and explain how de Bruijn graphs, string graph, etc. all came together.
Gene Myers made major contribution to genomics as the author of Celera assembler and as a co-author of Stephen Altschul’s BLAST paper. In fact, we argued elsewhere (but cannot locate even with Google’s help) that if a Nobel prize is ever awarded for the human genome, he should get it alone. However, if the Nobel committee decides to pick a group, he needs to share the award with all Celera stockholders, who bought the stock in March 2000 !!
Those working on next-gen sequencing also benefit greatly from his another contribution that does not get mentioned too often. His 1990 paper with Udi Manber got the ball rolling on suffix arrays by introducing a simple, space- efficient alternative to suffix trees. That concept, combined with Burrows Wheeler transform and FM index, got incorporated into all modern short read aligners. We discussed the history two years back in the following link.
Burrows Wheeler transform, Suffix Arrays and FM Index
How could one person make so many fundamental contributions in both genome assembly and sequence alignment? For that, you need to dig into the 1991 doctoral dissertation of John D. Kececioglu, which contains a lot of intellectual groundwork for his later contributions.
Exact and approximation algorithms for DNA sequence reconstruction
Also, it is not coincidental that Kececioglu had both Manber and Myers on his thesis committee (will explain later).

-—————————————————-
**Prior Approach - Shortest Common Superstring Problem (SCS) **
Prior to Myers’ work in 1990, computer scientists treated fragment assembly as a ‘shortest common superstring problem’ and tried to develop various algorithms to work around sequencing error rate within that framework.
In computer science, the shortest common supersequence problem is a problem closely related to the longest common subsequence problem. Given two sequences X = < x1,…,xm > and Y = < y1,…,yn >, a sequence U = < u1,…,uk > is a common supersequence of X and Y if U is a supersequence of both X and Y. In other words, the shortest common supersequence between strings x and y is the shortest string z such that both x and y are subsequences of z.
The shortest common supersequence (scs) is a common supersequence of minimal length. In the shortest common supersequence problem, the two sequences X and Y are given and the task is to find a shortest possible common supersequence of these sequences. In general, the scs is not unique.
For two input sequences, an scs can be formed from a longest common subsequence (lcs) easily. For example, if X[1..m] = abcbdab and Y[1..n] = bdcaba, the lcs is Z[1..r] = bcba. By inserting the non-lcs symbols while preserving the symbol order, we get the scs: U[1..t] = abdcabdab.
SCS is a nice computer science problem, but there was one small difficulty in using it for genome assembly. Real genomes were far more irrational than ‘shortest common supersequence’, because they contained repeats, ALUs and bunch of unexpected and unnecessary elements commonly known as junk DNA. This irrationality continues to bother computer scientists (like Ewan Birney) so much that they periodically kill junk DNA, only to be resurrected by Dan Graur.
The following figure from Myers’ 1995 paper shows why SCS fails for genome assembly.
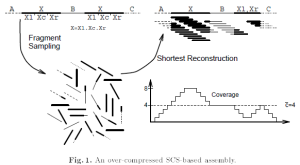
Kececioglu’s major contribution was to redefine the problem and add an expectation maximization step to decide which reconstructed string would be the best fit for a given fragment collection. That reconstructed string did not have to always be shortest common superstring. The proposed assembly steps had similarities with Peltola’s 1984 paper and is currently recognized as overlap-layout-consensus paradigm.
-—————————————————-
Suffix Arrays
It was not a coincidence that Manber and Myers (two of Kececioglu’s committee members) were thinking about suffix arrays at the same time they were working on fragment assembly algorithms. Myers’ assembly algorithm constituted of aligning the ends of every pair of reads and that meant their number of suffix-prefix matches scaled quadratically with the number of reads. Therefore, addressing the scalability of alignment problem was important, if they wanted to apply their method on large genomes.
Twenty years later, Jared Simpson struggled with the same problem, when he wanted to develop a string graph assembler for short reads. His first SGA paper presented an elegant approach to align the ends of reads, as we discussed in an earlier commentary (String Graph Assembler).
Why did nobody else try similar approach before?
It is because the computation of overlaps between all read pairs is very time- consuming. The most important innovation of Simpson-Durbin approach comes into reducing this computational time from quadratic order to linear order of the number of reads (or rather their sequence length). They achieved it by representing the reads as suffix array, and then finding the overlaps using FerraginaManzini index (FM-index) derived from the BurrowsWheeler transform. The core of Simpson-Durbin algorithm, where they presented the above step, is available from an earlier paper. In the latest paper, they described use of their technique on mammalian-sized sequence data.
-—————————————————-
de Bruijn Graph Algorithm
Myers was not the only person thinking about genome assembly in those days. Michael Waterman, who was famous as a computational biologist for his work with Temple Smith (Smith-Waterman algorithm), published a seminal mathematical paper in 1988 with Eric Lander. That paper gave the initial formulation for what the right coverage needed to be for a large genome project (check mention of ‘Poisson distribution’ in Myers’ Dazzle talk).
Genomic mapping by fingerprinting random clones: a mathematical analysis
Results from physical mapping projects have recently been reported for the genomes of Escherichia coli, Saccharomyces cerevisiae, and Caenorhabditis elegans, and similar projects are currently being planned for other organisms. In such projects, the physical map is assembled by first “fingerprinting” a large number of clones chosen at random from a recombinant library and then inferring overlaps between clones with sufficiently similar fingerprints. Although the basic approach is the same, there are many possible choices for the fingerprint used to characterize the clones and the rules for declaring overlap. In this paper, we derive simple formulas showing how the progress of a physical mapping project is affected by the nature of the fingerprinting scheme. Using these formulas, we discuss the analytic considerations involved in selecting an appropriate fingerprinting scheme for a particular project.
Waterman also started working on his own assembly algorithm in collaboration with Pavel Pevzner and Ramana Idury. In 1994, in two back-to-back talks at a DIMACS workshop on computational biology, Myers and Idury/Waterman presented their alternate approaches. Idury/Waterman method later came to be known as the de Bruijn graph algorithm.
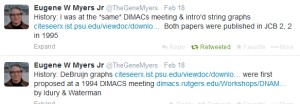
Contents of those talks were published in two back-to-back papers published in a new journal - Journal of Computational Biology.
-—————————————————-
Which one was Superior Approach?
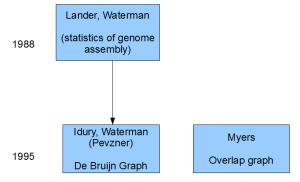
If scientists were asked to bet on one of the two approaches in 1995, they would have chosen one proposed by Waterman. Not only Waterman was famous for his Smith-Waterman algorithm, but he also ‘understood genome assembly’ based on his published work with Lander. Moreover, the de Bruijn graph approach presented by them (build a graph of k-mers and then identify Eulerian path) appeared mathematically elegant.
However, unlike Waterman, Myers had all ducks properly lined up and those were (i) a nice and compact overlap graph, (ii) statistical framework, (iii) alignment algorithm to scale up his method. In retrospect, anyone comparing Kececioglu’s 1991 thesis with 1995 paper by Idury/Waterman can understand that Myers was way ahead at that time, although it was not clear in 1995. In a Biostar comment on review of genome assembly papers, Heng Li described Myers as ‘a legendary figure in computional biology’. Myers is considered legendary, because nobody in 1995 expected him to succeed !!
-—————————————————-
Birth of Bioinformatics as a Field
As an aside, RECOMB conference was started in 1998 by Waterman, Pevzner and Sorin Istrail (author of HapCompass paper among many contributions, check HapCompass: An Elegant Use of Graphs for Haplotype Assembly/Phasing). That could possibly be considered the beginning of ‘bioinformatics’ as a branch of computer science.
Pevzner continues to come up with innovative educational tools to teach bioinformatics. Check Rosalind and his Coursera course for example. Ruibang Lou of BGI told us that online methods like Rosalind and Coursera are having big impact in China, because the students do not need to go through myriads of visa hoops to move to USA, so that they could join US universities to get advanced education.
Waterman went one step ahead in that regard and moved to China to start a bioinformatics program at Tsinghua University.
Istrail was our collaborator a few years back on a Science paper, and at that time he expressed desire to learn biology at the bench. We do not know how much progress he made on that front, but, apart from that, he had been involved with Algorithmic Biology lab in Russia.
-—————————————————-
Celera Assembler
Back to the genome assembly story.
(To be continued….)
In part (ii), of this commentary, we will cover Celera assembler, de Bruijn graph paper and Euler assembler by Pevzner, Velvet, SOAP-denovo and SPAdes leading up to Dazzler. We will also comment on the disagreements we had with Gene Myers in twitter.