Search Score and E-value

When we allow for imperfections and gaps in mapping, an infinite number of alternatives become acceptable. Search score and expectation values are two parameters to separate the wheat from the chaff. Let us give few examples to explain what they measure.

Suppose you are looking for the word ‘US’ in reference word ‘HOMOLOG.US’. That search is easy, because you can easily locate ‘US’ at the tail end of the reference.

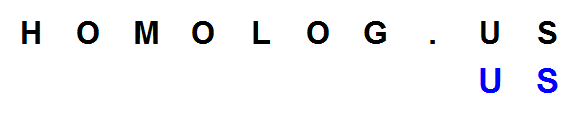
Next, we look for the word ‘MOO’ within ‘HOMOLOG.US’. That is a bit more complicated, because ‘MOO’ can be found only after we allow for a gap.

Guess what, we will find ‘YOU’ within ‘HOMOLOG.US’ next. Impossible, do you think? Well our answer is shown below. It allows for one mismatch and two gaps.

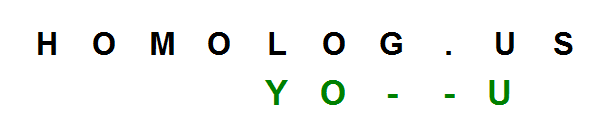
Nobody thinks the last match is genuine, but how do we mathematically establish that point? Search score and expectation value come to the rescue.

Score Suppose we give 5 points for perfect match of a letter, 1 point for imperfect match and -5 points for gap-opening. The score for map of ‘US’ is 10, because it includes two perfect matches. The score for ‘MOO’ is 53-5=10 as well, but the score for ‘YOU’ is a lousy 1+5+5-52=1. That shows that ‘US’ and ‘MOO’ are far better matches than ‘YOU’.

E-value You may have noticed that ‘YOU’ will get at least 3 points in our scoring system no matter where we place it as long as all its letters are all together. The assignment of 1 for each imperfect match is not a good idea. Similarly, one may argue that a gap penalty of -5 is too harsh. Overall, any scoring system has some degree of arbitrariness and therefore the total score is not a good measure to compare searches by different programs. Expectation value removes the arbitrariness by expressing the score as a probability. It computes the probability that the match is found by chance alone within the reference sequence.