Reversibility of BWT

We mentioned that BWT is reversible. How do we go back from the following sequence to ‘homolog.us$’ ?

Please note that the above sequence comes from the last column of matrix to derive BWT, but we also know another column, the first one. The first column has all characters of the last column sorted alphabetically.

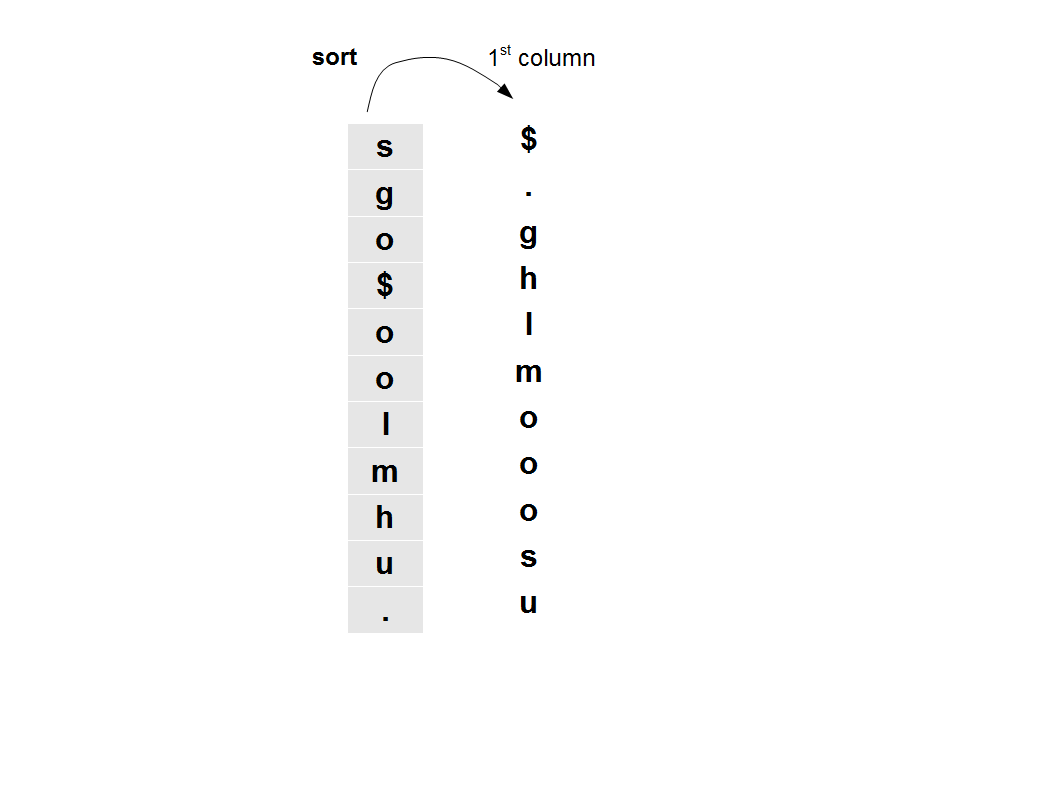
What else do we know? We know that, in the original word, the characters in the first column follow the characters in the last column. So, we know that in the original word ‘s’ is followed by ‘$’, ‘g’ is followed by ‘.’, ‘o’ is followed by ‘g’, ‘$’ is followed by ‘h’, ‘o’ is followed by ‘l’ and so on.

The letter followed by $ is the first word. That is ‘h’. Then comes ‘o’ from the above table. What comes after ‘o’? We have three choices – ‘g’, ‘l’ and ‘m’. This is where we need to invoke the LF mapping property. We know that ‘h’ is followed by the last ‘o’ in the 1st column. The last ‘o’ of th BWT column is followed by ‘m’. Pretty neat, huh? You can reconstruct the entire sequence in this manner.