Note: These tutorials are incomplete. More complete versions are being made available for our members. Sign up for free.

Generalized Definition of de Bruijn graph
The concept of de Bruijn graph came from graph theory and has broader application beyond bioinformatics. For the sake of completeness, in this subsection, we define de Bruijn graphs in the most general mathematical terms. Readers, who find the discussion abstract, may skip to next section without any loss of understanding.
A generalized definition of de Bruijn graph relies on a set of m symbols and n dimensions. For bioinformatics applications related to nucleotides, the set of symbols consist of four characters (‘A’, ‘C’, ‘T’, ‘G’) and dimension is equivalent to the chosen k-mer size.
A generalized de Bruijn graph is a directed graph, where an edge exists from all nodes of form A=(a1, a2, a3, ….an) to B=(b1,b2,b3,….bn) with B being a left-shifted version of A, or b1=a2, b2=a3,…..bn-1=an. In simple language of the previous section, it means that two connected nodes have overlaps of n-1 ‘nucleotides’.
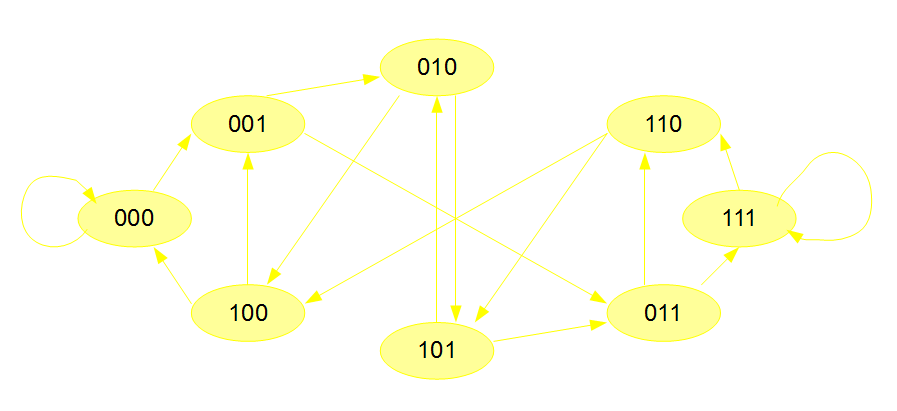
As an example, we choose an alphabet with two symbols ‘0’ and ‘1’, and select dimension=3. With two possible symbols and each node being made of three symbols, 2^3=8 words can be formed. They are 000, 001, 010, 011, 100, 101, 110, 111. The complete de Bruijn graph with those 8 nodes is shown below. In the graph, two nodes are connected as (A → B), only if the last 2 symbols of A are the same as the first two symbols of B. The same rule can be generalized to construct de Bruijn graph with k dimensions. In such a de Bruijn graph, an edge is drawn between (A-> B), if the last k-1 symbols of node A are the same as the first k-1 symbols of node B.
The difference between the generalized de Bruijn graph shown above and the de Bruijn graph for a genome presented in previous section is that, for the genome, we did not display all 4^k nodes and instead focused only on k-mer nodes present in the genome. De Bruijn graphs for various genomes with k-mer nodes are subgraphs of the most generalized and complete de Bruijn graph of dimension k. Another important difference between mathematical de Bruijn graphs of symbols, and de Bruijn graph constructed from nucleotides is discussed in the following section.
